Laboratorio 5 - Parte 1. Redes recurrentes#
!wget -nc --no-cache -O init.py -q https://raw.githubusercontent.com/jdariasl/Intro_ML_2025/master/init.py
import init; init.init(force_download=False); init.get_weblink()
from local.lib.rlxmoocapi import submit, session
import inspect
session.LoginSequence(endpoint=init.endpoint, course_id=init.course_id, lab_id="L05.01", varname="student");
#configuración del laboratorio
# Ejecuta esta celda!
from Labs.commons.utils.lab5 import *
_, dataset = part_1()
En este laboratorio entrenaremos una Red Neuronal Recurrente para la predicción de una serie de tiempo.
Este problema corresponde a una configuración many-to-one.
En este caso usaremos una serie de tiempo que corresponde al número de pasajeros internacionales por mes, desde el año 1949 hasta el año 1960.
En la siguiente celda visualizamos los datos.
Debemos observar el aparente periodo que existe en nuestra variable. ¿cada cuantos meses parece repertirse el patrón de la serie?
# creamos una variable para
# el tiempo
Time = pd.date_range(np.datetime64('1949-01'), np.datetime64('1961-01'), freq='M')
print("tenemos dispnible nuestra base de datos en el pandas DF 'dataset' \n")
fig, ax = plt.subplots(figsize = (16,6))
ax.plot(Time,dataset)
ax.set_title('International airline passengers')
ax.set_xlabel('Time (months)')
ax.set_xticks( pd.date_range(np.datetime64('1949-01'), np.datetime64('1961-01'), freq='3M'))
plt.xticks(rotation=90)
plt.show()
En nuestro primer ejercicio vamos a explorar, el patrón que observamos en la grafica anterior. Esto tambien nos puede decir qué relación existe entre una muestra en el tiempo \(t\) con las muestras anteriores.
La libreria statsmodel tiene una función que nos sirve para analizar esta relación.
Ejercicio 1 - Exploración del problema#
Este plot realiza una operación cuyos detalles son explicados en mayor profundidad en esta buena entrada de blog. Pero en este laboratorio lo que no interesa entender es:
El valor varia entre 1.0 y -1.0.
Cuando el valor de la correlación es 1.0, corresponde el valor maximo indicando una relación positiva entre la variable y su correspondiente lag o retraso.
Cuando el valor de la correlación es -1.0, corresponde el valor mínimo indicando una relación negativa entre la variable y su correspondiente lag o retraso..
0.0 indica que los valores no están relacionados.
el lag indica, el número de retrasos. Si el valor de la correlación en el lag 5 es igual 0.75, indica una relación positiva alta entre el actaul y el quinto retraso anterior en la mayoria de muestras de nuestra variable de respuesta.
Ahora, grafiquemos la correlación para un maximo de 36 lags de nuestros datos. Esto significa que estamos analizando las relación de una muestras respecto a la 36 muestras pasdas.
Sabiendo que nuestro eje X representa los meses y nuestro eje y representan el numero de pasajeros. Al realizar el analisis de lags estamos determinando si el número de pasajeros de los meses pasados tiene influencia en el nuúmero de pasajeros en el mes acutal.
from statsmodels.graphics import tsaplots
fig, ax = plt.subplots(figsize = (12,7))
# Display the autocorrelation plot of your time series
fig = tsaplots.plot_acf(dataset.passengers, lags=range(1,37), ax = ax)
ax.set_xticks( range(1,37))
ax.scatter(range(0,37,12), 0.1*np.ones(4), c = 'r', marker = "v")
plt.show()
reforzando el entendimiento, observando la grafica anterior:
Cuando hay un lag = 5 (es decir se evalúa qué tan relacionadas están las 5 muestras anteriores), tenemos una autocorrelación \(\approx\) 0.75
Cuando hay un lag = 25 (es decir se evalúa qué tan relacionadas están las 25 muestras anteriores), tenemos una autocorrelación \(\approx\) 0.5
Presta atención al patrón que se resalta con las marcas rojas
Vamos a observar estas relaciones viendo cómo los picos de correlación se relacionan con los patrones que vemos. A continuación, graficamos los valores de autocorrelación junto con la serie de los valores reales.
fig, ax = plt.subplots(figsize = (12,7))
# Display the autocorrelation plot of your time series
fig = tsaplots.plot_acf(dataset.passengers, lags=range(1,37), ax = ax)
ax.set_xticks( range(1,37))
ax.set_ylabel("Valor de correlación")
ax2 = ax.twinx()
ax2.set_ylabel("Numero de pasajeros")
ax2.plot(dataset[0:37], c = 'r')
plt.show()
Ahora bien, para poder aplicar una RNN, debemos transformar los datos. Observa la figura, para entender como debemos transformar los datos.
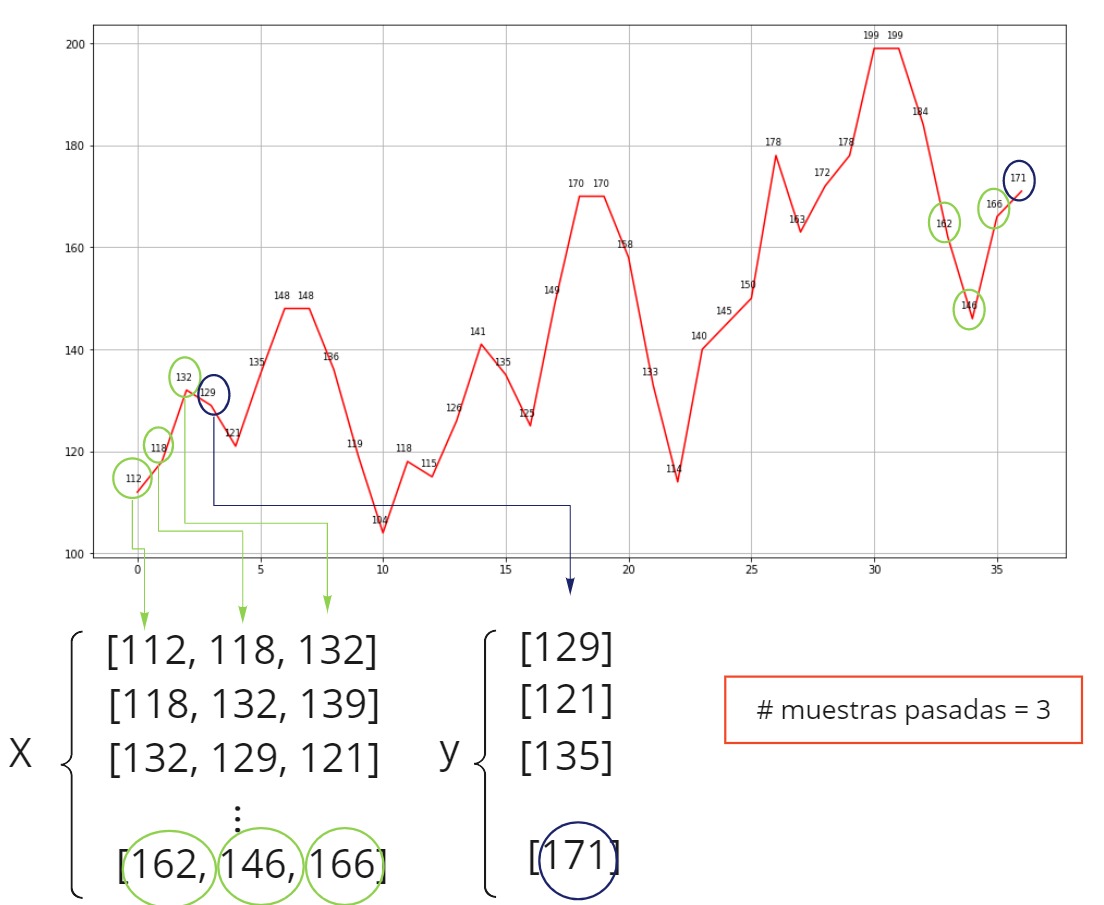
Con base en el análisis de correlación que reveló cómo están relacionadas la muestra actual y las anteriores y teniendo en cuenta que la preparación de los datos consiste en usar las muestras pasadas para predicir la muestra siguiente. Responde la siguiente pregunta.
#@title Pregunta Abierta
#@markdown ¿Cual podría ser el número máximo de muestras pasadas para transformar el conjunto de datos?
respuesta = "" #@param {type:"string"}
Ahora, realicemos el ejercicio de transformar nuestros datos a la forma requerida.
#ejercicio de codigo
def create_dataset(dataset, look_back=1):
"""función que crea dataset apto para RNN
dataset: matriz numpy con el conjunto de datos
look_back: número de retrasos con los cuales queremos construir
las características
Retorna:
X: un numpy array con los valores de entrada a la red (debe ser una matrix)
Y: un numpy array con los valores de salida deseada de la red
"""
return X, Y
Registra tu solución en línea
student.submit_task(namespace=globals(), task_id='T1');
# observemos el funcionamiento de nuestra funcion
x_to_see, y_to_see = create_dataset(dataset.values, 3)
display("primeras muestras de x", x_to_see[0:3])
display("primeras muestras de y", y_to_see[0:3])
Ejercicio 2 - Crear una RNN#
Al igual que en laboratorio anterior, vamos a usar PyTorch para diseñar y construir las redes neuronales con las que vamos a experimentar.
En el siguiente ejercicio vamos a crear una función para construir una RNN usando la libreria mencionada. Deben revisar con detenimiento la documentación de las capas tipo RNN.
# ejercicio de código
# Vamos a crear una red neuronal recurrente. En este caso no podemos usar el módulo
# nn.Sequential porque las capas RNN retornan dos salidas y es necesario, según el
# diseño de la arquitectura, decidir cómo usarlas.
def create_rnn_model(num_hidden_neurons):
import torch.nn as nn
"""función que crea un modelo RNN
La arquitectura de la red RNN debe estar compuesta de dos capas:
1. Una capa RNN (tener en cuenta el número de neuronas ocultas,
como vamos a modelar una serie temporal unidimensional, el número de características es 1)
2. Una capa Densa (Linear) de salida
parametros
num_hidden_neurons (int): número neuronas en la capa oculta
retorna nn.Module con la red neuronal
"""
class Recurrent_NN(nn.Module):
def __init__(self, num_hidden_neurons):
super().__init__()
self.rnn = ...
self.linear =...
#Este método define el fluje de información a través del modelo
def forward(self, x):
_, h = self.rnn(x)
x = h.squeeze()
x = self.linear(x)
return x
return Recurrent_NN(num_hidden_neurons)
Registra tu solución en línea
student.submit_task(namespace=globals(), task_id='T2');
#Grafiquemos las arquitecturas de dos modelos con parámetros diferentes:
import torch
from torchview import draw_graph
input_data = np.random.randn(100)
look_back = 2
X, _ = create_dataset(input_data,look_back=look_back)
X = torch.from_numpy(X).float()
# Una capa RNN recibe entradas de dimensión (Batch,Tiempo,Dimensión). En realidad queremos que los
# retardos sean entendidos como muestras pasadas (Tiempos), por lo tanto agregamos
# una dimensión al final para que el modelo lea los datos como valores pasados de 1
# dimensión.
X = X.unsqueeze(2)
model = create_rnn_model(num_hidden_neurons = 10)
model_graph = draw_graph(model, input_size=X.shape)
model_graph.visual_graph
look_back = 4
X, _ = create_dataset(input_data,look_back=look_back)
X = torch.from_numpy(X).float()
X = X.unsqueeze(2)
model = create_rnn_model(num_hidden_neurons = 5)
model_graph = draw_graph(model, input_size=X.shape)
model_graph.visual_graph
Ejercicio 3: Experimentar con RNN#
Con nuestra función que crea modelos, vamos experimentar variando los dos parametros:
número de retrasos
número de neuronas en la capa oculta
Otras condiciones:
Vamos a dejar fijo el # de epocas 50.
Usaremos la métrica MAE (ver sklearn)
#ejercicio de código
def experimentar_rnn(data, look_backs, hidden_neurons):
"""función que realiza experimentos para evaluar una RNN de elman usando
el error absoluto medio como medida de error
data: pd.Dataframe, dataset a usar
look_back: List[int], lista con los número de retrasos a evaluar
hidden_neurons: List[int], list con el número de neuronas en la capa oculta
retorna: pd.Dataframe con las siguientes columnas:
- lags
- neuronas por capas
- error de entrenamiento
- error de prueba
"""
# Normalizar
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(data)
# realizar el split
train_size = int(len(dataset) * 0.7)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
resultados = pd.DataFrame()
idx = 0
for num_hidden_neurons in hidden_neurons:
for look_back in look_backs:
# aplicar la transformación creada antes
trainX, trainY = ...
trainX = torch.from_numpy(trainX).float()
trainY = torch.from_numpy(trainY).float()
trainX = trainX.unsqueeze(2)
testX, testY = ...
testX = torch.from_numpy(testX).float()
testX = testX.unsqueeze(2)
# creemos el modelo
model = ...
# Defina la función de coste de mean absolute error en PyTorch
loss = torch.nn...
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
#Entrenaremos el modelo por 50 epocas
for epoch in range(50):
model.train()
optimizer.zero_grad()
trainYPred = model(trainX)
trainLoss = loss(trainYPred, trainY)
trainLoss.backward()
optimizer.step()
# Obtener las predicciones del modelo
model.eval()
trainYPred = ...
testYPred = ...
#Use la métrica de error absoluto medio de sklearn
#Note que usamos el método detach() para poder usar la función de sklearn
errorEntrenamiento = ...(trainY.detach().numpy(), trainYPred.detach().numpy())
errorPrueba = ...(testY, testYPred.detach().numpy())
resultados.loc[idx,'lags'] = look_back
resultados.loc[idx,'neuronas por capa'] = ...
resultados.loc[idx,'error de entrenamiento'] = ...
resultados.loc[idx,'error de prueba'] = ...
idx+=1
print("termina para", look_back, num_hidden_neurons)
return (resultados)
Registra tu solución en línea
student.submit_task(namespace=globals(), task_id='T3');
Ahora vamos a ver los resultados del experimento:
variando los lags dejando las neuronas por capa fijas
variando las neuronas y dejando los retrasos fijos
Si la semilla no se ajusta los resultados pueden cambiar debido a la inicialización aleatoria de la red y al tamaño limitado de la serie de tiempo.
# observa el comportamiento de los lags
import seaborn as sns
import torch.nn as nn
import torch
torch.manual_seed(2)
np.random.seed(2)
resultadosRNN = experimentar_rnn(dataset, look_backs = [3,9,12,24,30,36], hidden_neurons=[15])
# plot
ax1 = sns.relplot(data= resultadosRNN, x= 'lags', y = 'error de prueba', kind = 'line', aspect = 2)
ax1.fig.suptitle('efecto del # retrasos')
torch.manual_seed(2)
np.random.seed(2)
resultadosRNN = experimentar_rnn(dataset, look_backs = [9], hidden_neurons=[5,15,30,60])
ax2 = sns.relplot(data= resultadosRNN, x= 'neuronas por capa', y = 'error de prueba', kind = 'line', aspect = 2)
ax2.fig.suptitle('efecto del # neuronas')
#@title Pregunta Abierta
#@markdown ¿Por qué seguir aumentando los tiempos de retardo no implica siempre una mejora en la predicción del modelo?
respuesta = "" #@param {type:"string"}
Ejercicio 4 - Comparación con MLP#
En este ejercicio vamos a resolver el mismo problema, pero con un MLP. Con esto vamos a comparar los resultados obtenidos con la RNN.
Seguiremos las siguientes reglas:
Variar el número de retrasos, que corresponden en este caso al número de características en la capa de entrada
Usaremos solo una capa oculta y evaluaremos diferente número de neuronas en esta capa
El número de epocas también se ajustará a 50
Usaremos las misma métrica y función de coste empleadas en el ejercicio anterior.
#ejercicio de código
def create_mlp_model(look_back, num_hidden_neurons):
''' función que retorna el modelo MLP con una sola capa oculta con función de activación ReLU
En este caso se puede volver a hacer uso del módulo nn.Sequential de pytorch
Recordar el ejercicio 4 del laboratorio 4 parte 1.
Parametros:
look_back: número de retrasos que serán usados como características de entrada
num_hidden_neurons: número de neuronas en la capa oculta
Retorna:
nn.Module con el modelo MLP
'''
return
def experimentar_MLP(data, look_backs, hidden_neurons):
"""función que realiza experimentos para evaluar una MLP usando
MAE como medida de error
data: pd.Dataframe, dataset a usar
look_back: List[int], lista con los numero de retrasos a evaluar
hidden_neurons: List[int], list con el numero de neuronas en la capa oculta
retorna: pd.Dataframe con las siguientes columnas:
- lags
- neuronas por capas
- error de prueba
- tiempo de entrenamiento
"""
# we need to normalize the dataset before
#
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(data)
# split into train and test sets
train_size = int(len(dataset) * 0.7)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
resultados = pd.DataFrame()
idx = 0
for num_hidden_neurons in hidden_neurons:
for look_back in look_backs:
trainX, trainY = create_dataset(train, look_back)
trainX = torch.from_numpy(trainX).float()
trainY = torch.from_numpy(trainY).float().reshape(-1,1)
testX, testY = create_dataset(test, look_back)
testX = torch.from_numpy(testX).float()
# creemos el modelo MLP
model = ...
# Defina la función de coste de mean absolute error en PyTorch
loss = torch.nn...
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
#Entrenaremos el modelo por 50 epocas
for epoch in range(50):
model.train()
optimizer.zero_grad()
trainYPred = model(trainX)
trainLoss = loss(trainYPred, trainY)
trainLoss.backward()
optimizer.step()
# Obtener las predicciones del modelo
model.eval()
trainYPred = ...
testYPred = ...
#Use la métrica de error absoluto medio de sklearn
#Note que usamos el método detach() para poder usar la función de sklearn
errorEntrenamiento = ...(trainY.detach().numpy(), trainYPred.detach().numpy())
errorPrueba = ...(testY, testYPred.detach().numpy())
resultados.loc[idx,'lags'] = look_back
resultados.loc[idx,'neuronas por capa'] = ...
resultados.loc[idx,'error de entrenamiento'] = ...
resultados.loc[idx,'error de prueba'] = ...
idx+=1
print("termina para", look_back, num_hidden_neurons)
return (resultados)
Registra tu solución en línea
student.submit_task(namespace=globals(), task_id='T4');
resultadosMLP = experimentar_MLP(dataset, look_backs = [3,9,12,24,30,36], hidden_neurons=[10,20,30])
# para ver los resultados
# en esta instrucción se va resaltar el menor error
resultadosMLP.style.highlight_min(color = 'green', axis = 0, subset = ['error de prueba'])
Ejercicio 5 - Construcción de modelo LSTM#
En nuestro ultimo ejercicio, vamos a crear una arquitectura de red con una capa LSTM en lugar de una capa RNN. (Ver la documentación de PyTorch sobre este tipo de capas link).
#@title Pregunta Abierta
#@markdown ¿Por qué una red LSTM puede ser más adecuada para resolver este problema?
respuesta = "" #@param {type:"string"}
#ejercicio de código
def create_lstm_model(num_hidden_neurons):
import torch.nn as nn
"""función que crea un modelo LSTM
La arquitectura de la red LSTM debe estar compuesta de dos capas:
1. Una capa LSTM (tener en cuenta el número de neuronas ocultas,
como vamos a modelar una serie temporal unidimensional, el número de características es 1)
2. Una capa Densa (Linear) de salida
parametros
num_hidden_neurons (int): número neuronas en la capa oculta
retorna nn.Module con la red neuronal
"""
class LSTM_net(nn.Module):
def __init__(self, num_hidden_neurons):
super().__init__()
self.lstm = ...
self.linear =...
#Este método define el fluje de información a través del modelo
def forward(self, x):
return
return LSTM_net(num_hidden_neurons)
Registra tu solución en línea
student.submit_task(namespace=globals(), task_id='T5');
look_back = 4
X, _ = create_dataset(input_data,look_back=look_back)
X = torch.from_numpy(X).float()
X = X.unsqueeze(2)
model = create_lstm_model(num_hidden_neurons = 5)
model_graph = draw_graph(model, input_size=X.shape)
model_graph.visual_graph
Una vez superada la prueba, pueden usar el modelo creado para realizar experimentación de manera similar al ejercicio 3. La función de experimentación es igual, simplemente es necesario reemplezar la función create_rnn_model por la nueva create_lstm_model y ejecutar los experimentos.

