TF symbolic engine#

!wget --no-cache -O init.py -q https://raw.githubusercontent.com/jdariasl/OTBD/main/content/init.py
import init; init.init(force_download=False)

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
%load_ext tensorboard

from sklearn.datasets import *
from local.lib.utils import make_graph
from IPython.display import Image
tf.__version__

2023-10-18 18:21:48.852776: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.

'2.14.0'

TF is a symbolic computing + optimization library for machine learning problems#

ML expressions involve:

  • variables representing data as n-dimensional objects

  • variables representing parameters as n-dimensional objects

  • mostly matrix operations (multiplications, convolutions, etc.)

  • some non linear operations (activation functions)

Recall that in sympy we FIRST define expressions (a computational graph) and THEN we evaluate them feed concrete values.

Tensorflow INTEGRATES both aspects so that building computational graphs LOOKS LIKE writing regular Python code as must as possible.

  • a tf.Variable represents a symbolic variable, that contains a value

See:

x = tf.Variable(initial_value=[7], name="x", dtype=tf.float32)
y = tf.Variable(initial_value=[9], name="y", dtype=tf.float32)
f = x**2+y**3
f

<tf.Tensor: shape=(1,), dtype=float32, numpy=array([778.], dtype=float32)>

f is SYMBOLIC EXPRESSION (a Tensor in TF terms) that also contains a value attached to it.

for which TF can obtain gradients automatically. This might seem a rather akward way of obtaining the gradient (with GradientTape). The goal is that you write code as in Python and TF takes care of building the computational graph with it.

with tf.GradientTape(persistent=True) as t:
    f = x**2 + y**3
    
print (t.gradient(f, x), t.gradient(f, y))
    

tf.Tensor([14.], shape=(1,), dtype=float32) tf.Tensor([243.], shape=(1,), dtype=float32)

print (t.gradient(f, [x,y]))

[<tf.Tensor: shape=(1,), dtype=float32, numpy=array([14.], dtype=float32)>, <tf.Tensor: shape=(1,), dtype=float32, numpy=array([243.], dtype=float32)>]

usually expressions are built within functions decorated with @tf.function for performance

@tf.function
def myf(x,y):
    return x**2 + y**3

with tf.GradientTape(persistent=True) as t:
    f = myf(x,y)
    
print (t.gradient(f, x), t.gradient(f, y))

tf.Tensor([14.], shape=(1,), dtype=float32) tf.Tensor([243.], shape=(1,), dtype=float32)

!rm -rf logs
make_graph(myf, x, y, logdir="logs")

<tensorflow.python.eager.polymorphic_function.polymorphic_function.Function object at 0x7fe930b92a00>

%tensorboard --logdir logs

Tensors#

in Tensorflow the notion of a Tensor is just a symbolic multidimensional array.

Observe how Tensorflow naturally deals with multidimensional symbolic variables (Tensors)

\[\frac{1}{n} \sum_{i=1}^n ({\bf{w}}^T{\bf{x}}_i - y_i)^2\]
n = 3
X = tf.Variable(initial_value=[[2, 6], [3, 1], [4, 5]], name="X", dtype=tf.float32)
w = tf.Variable(initial_value=[[-2],[1]], name="w", dtype=tf.float32)
y = tf.Variable(initial_value=[[8],[2],[3]], name="y", dtype=tf.float32)

with tf.GradientTape(persistent=True) as t:
    f = tf.reduce_mean((tf.matmul(X,w)-y)**2)
    
g = t.gradient(f, w)
g

<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[-38.      ],
       [-48.666668]], dtype=float32)>

But a tf.Tensor is always a symbolic variable. In order to reconcile symbolic and execution worlds, Tensorflow attaches a value to each symbolic variable, and carries it forward when making derivations.

  • X, y and w are Tensors that we define with a specific value

  • g is a Tensor derived from X, y and w that have ALSO been evaluated with the corresponding values.

g.numpy()

array([[-38.      ],
       [-48.666668]], dtype=float32)

Implementing linear regresion in TF#

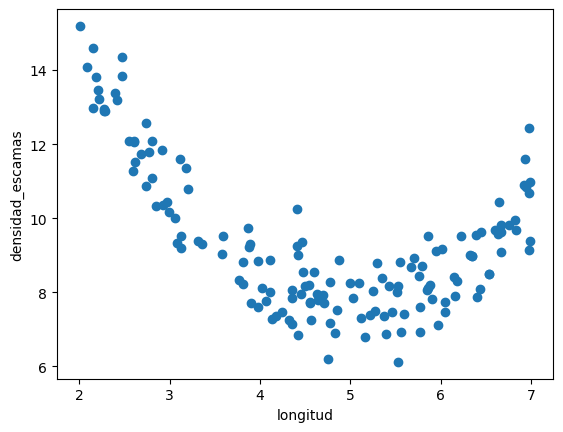
d = pd.read_csv("local/datasets/trilotropicos.csv")
y = d.densidad_escamas.values.astype(np.float32)
X = np.r_[[d.longitud.values]].T.astype(np.float32)

print(X.shape, y.shape)
plt.scatter(d.longitud, d.densidad_escamas)
plt.xlabel(d.columns[0])
plt.ylabel(d.columns[1]);

(150, 1) (150,)
../_images/2e8b795093074d54cc1c3d282f240d392d701404fc7af910dc46ef1cdbda11cf.png 
from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X,y)
lr.coef_, lr.intercept_

(array([-0.71805906], dtype=float32), 12.689999)

Version 1: raw low level with gradient descent#

  • beware of typing. tensorflow is very sensitive to numeric data types (tf.float32, tf.float64, etc.) Default types in numpy and tensorflow might not always be the same

from tqdm import tqdm
epochs = 4000
learning_rate = 0.01

# symbolic variables
w = tf.Variable(np.random.normal(size=(X.shape[-1], 1), scale=.6), dtype=tf.float32)
b = tf.Variable(np.random.normal(size=(1,), scale=.6), dtype=tf.float32)
h = []

#optimization loop
for epoch in tqdm(range(epochs)):
    with tf.GradientTape() as t:
        preds = tf.matmul(X,w)+b
        loss = tf.reduce_mean( (preds-y.reshape(-1,1))**2)
        
    gw, gb = t.gradient(loss, [w, b])
    
    w.assign_sub(learning_rate * gw)
    b.assign_sub(learning_rate * gb)
    
    h.append([gw.numpy()[0][0], gb.numpy()[0], w.numpy()[0][0], b.numpy()[0], loss.numpy()])
h = np.r_[h]
print (b.numpy(), w.numpy())

100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 4000/4000 [00:07<00:00, 524.88it/s]

[12.678487] [[-0.7157973]]



rmse = tf.reduce_mean((tf.matmul(X,w)+b-y)**2).numpy()
plt.figure(figsize=(15,2));
plt.plot(h[:,-1]); plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse);
plt.ylim(0,50)

(0.0, 50.0)
../_images/8bf2b954b9c4e8178526643f39ddf9fd421b77ccd8115cef2753e09c6f2f40d5.png

Version 2: using tf.function to speed up#

epochs = 4000

# initialize weights
w.assign(np.random.normal(size=(X.shape[-1],1)).astype(np.float32)*.6) 
b.assign(np.random.normal(size=(1,)).astype(np.float32))

@tf.function
def get_gradient(w, b, X, y):
    with tf.GradientTape() as t:
        preds = tf.matmul(X,w)+b
        loss = tf.reduce_mean( (preds-y)**2)
        
    gw, gb = t.gradient(loss, [w, b])
    return gw, gb, loss

#optimization loop
h = []
for epoch in tqdm(range(epochs)):
        
    gw, gb, loss = get_gradient(w, b, X, y.reshape(-1,1))
    
    w.assign_sub(learning_rate * gw)
    b.assign_sub(learning_rate * gb)

    h.append([gw.numpy()[0][0], gb.numpy()[0], w.numpy()[0][0], b.numpy()[0], loss.numpy()])
h = np.r_[h]

print (b.numpy(), w.numpy())

100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 4000/4000 [00:04<00:00, 840.83it/s]

[12.6763935] [[-0.7153859]]

predictions = tf.matmul(X,w)+b

rmse = tf.reduce_mean((predictions-y)**2).numpy()
plt.figure(figsize=(15,2));
plt.plot(h[:,-1]); plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse);
plt.ylim(0,50)

(0.0, 50.0)
../_images/3248746f600937a8eb912b689a6bb003a69a54ea9323d0d899fa5b568ac89a85.png

Version 3: using batches with random shuffling (stochastic gradient descent)#

notice we tune the number of epochs as the number of weights updates increases

#optimization loop
batch_size = 16
epochs = 400

# initialize weights
w.assign(np.random.normal(size=(X.shape[-1],1))*.6) 
b.assign(np.random.normal(size=(1,)))

h = []

for epoch in tqdm(range(epochs)):
    
    idxs = np.random.permutation(len(X))
    
    for step in range(len(X)//batch_size+((len(X)%batch_size)!=0)):
        
        X_batch = X[idxs][step*batch_size:(step+1)*batch_size]
        y_batch = y[idxs][step*batch_size:(step+1)*batch_size]
        
        gw, gb, loss = get_gradient(w, b, X_batch, y_batch.reshape(-1,1))

        w.assign_sub(learning_rate * gw)
        b.assign_sub(learning_rate * gb)
        
        h.append([gw.numpy()[0][0], gb.numpy()[0], w.numpy()[0][0], b.numpy()[0], loss.numpy()])
h = np.r_[h]
print (b.numpy(), w.numpy())

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 400/400 [00:04<00:00, 85.38it/s]

[12.667722] [[-0.71434104]]



predictions = tf.matmul(X,w)+b

rmse = tf.reduce_mean((predictions-y)**2).numpy()
plt.figure(figsize=(15,2));
plt.plot(h[:,-1]); plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse);
plt.ylim(0,50)

(0.0, 50.0)
../_images/ce22c84988948cef104a50f3ef2628d8ecc26eefd346ccd711e47f1aead98a30.png

Version 4: packing up with Keras class API and custom SGD#

observe:

  • thebuild method that is called by Keras whenever input_shape is known

  • we use add_weight so that our model weights are known to the Keras model framework (trainable_variables, get_weights, etc.)

see here

class LinearRegressionModel4(tf.keras.Model):
    
    def build(self, input_shape):
        self.w = self.add_weight(shape=(input_shape[-1], 1), initializer='random_normal',
                                 trainable=True, dtype=tf.float32)
        
        self.b = self.add_weight(shape=(1,), initializer='random_normal',
                                 trainable=True, dtype=tf.float32)
        
    def call(self, inputs):
        return tf.matmul(inputs, self.w) + self.b
    
    @tf.function
    def get_gradient(self, X, y):
        with tf.GradientTape() as t:
            loss = tf.reduce_mean( (self(X)-y)**2)

        gw, gb = t.gradient(loss, [self.w, self.b])
        return gw, gb, loss

    def fit(self, X,y, epochs, batch_size=16, learning_rate=0.01):
        y = y.reshape(-1,1)
        self.h=[]
        for epoch in tqdm(range(epochs)):
            idxs = np.random.permutation(len(X))
            for step in range(len(X)//batch_size+((len(X)%batch_size)!=0)):
                X_batch = X[idxs][step*batch_size:(step+1)*batch_size]
                y_batch = y[idxs][step*batch_size:(step+1)*batch_size]            

                gw, gb, loss = self.get_gradient(X_batch,y_batch)
                self.w.assign_sub(learning_rate * gw)
                self.b.assign_sub(learning_rate * gb)
                self.h.append([gw.numpy()[0][0], gb.numpy()[0], w.numpy()[0][0], b.numpy()[0], loss.numpy()])
        self.h = np.r_[self.h]

model = LinearRegressionModel4()

observe that we can use the object directly on data to get predictions

model(X[:2])

<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[-0.14747247],
       [-0.119949  ]], dtype=float32)>

or with the .predict method

model.predict(X[:2])

1/1 [==============================] - 0s 60ms/step

array([[-0.14747247],
       [-0.119949  ]], dtype=float32)

model.trainable_variables

[<tf.Variable 'linear_regression_model4_2/Variable:0' shape=(1, 1) dtype=float32, numpy=array([[-0.01655438]], dtype=float32)>,
 <tf.Variable 'linear_regression_model4_2/Variable:0' shape=(1,) dtype=float32, numpy=array([-0.08428116], dtype=float32)>]

model.get_weights()

[array([[-0.01655438]], dtype=float32), array([-0.08428116], dtype=float32)]

and fit the model

model.fit(X, y, epochs=400, batch_size=16)

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 400/400 [00:04<00:00, 81.99it/s]

model.b.numpy(), model.w.numpy()

(array([12.6649475], dtype=float32), array([[-0.6100817]], dtype=float32))

predictions = model(X)

rmse = tf.reduce_mean((predictions-y)**2).numpy()
plt.figure(figsize=(15,2));
plt.plot(model.h[:,-1]); plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse);
plt.ylim(0,50)

(0.0, 50.0)
../_images/6ed7a01af7fd265a588f53ca20d6b8660d52e7801c8eea7476bb513c1eab0cf9.png

Version 5: Sequential Keras model with standard loop#

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
    
def get_model5():
    model = Sequential()
    model.add(Dense(1, input_shape=(X.shape[-1],), activation="linear"))
    model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.01), 
                  metrics=["mean_absolute_error"],
                  loss="mse")
# equivalent forms for loss    
#                  loss = lambda y_true, y_pred: tf.reduce_mean((y_true-y_pred)**2))
#                  loss="mean_squared_error")
#                  loss=tf.keras.metrics.mean_squared_error)
    return model

from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X,y.reshape(-1,1), test_size=0.2)
X_train.shape, X_val.shape, y_train.shape, y_val.shape

((120, 1), (30, 1), (120, 1), (30, 1))

!rm -rf logs
model = get_model5()

tb_callback = tf.keras.callbacks.TensorBoard('./logs', update_freq=1)
model.fit(X_train,y_train, epochs=100, batch_size=5, verbose=0, 
          callbacks=[tb_callback], validation_data=(X_val, y_val))

model.weights

[<tf.Variable 'dense_5/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[-0.6312059]], dtype=float32)>,
 <tf.Variable 'dense_5/bias:0' shape=(1,) dtype=float32, numpy=array([12.774989], dtype=float32)>]

history is now logged only per epoch

model.history.history.keys()

dict_keys(['loss', 'mean_absolute_error', 'val_loss', 'val_mean_absolute_error'])

predictions = model(X)
rmse = np.mean((predictions-y)**2)

plt.figure(figsize=(15,2));
plt.plot(model.history.history["val_loss"], label="val"); 
plt.plot(model.history.history["loss"], label="train"); 
plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse); plt.legend();
../_images/3916d6162d2ea21fe19b9ebeae19892dbfe223af1df8af50a1f6274f3f03a447.png 
mae = np.mean(np.abs(predictions-y))

plt.figure(figsize=(15,2));
plt.plot(model.history.history["val_mean_absolute_error"], label="val"); 
plt.plot(model.history.history["mean_absolute_error"], label="train"); 
plt.xlabel("step number"); plt.ylabel("MAE"); plt.grid();
plt.title("MAE %.3f"%mae); plt.legend();
../_images/670ac83cee609c7b8090ca27ce60d20037ee25ffa039b21680aa87542631eb73.png 
%tensorboard --logdir logs

Reusing TensorBoard on port 6006 (pid 47595), started 16:14:07 ago. (Use '!kill 47595' to kill it.)

Version 6: Custom model with Keras class API and standard loop#

class LinearRegressionModel6(tf.keras.Model):
    
    def build(self, input_shape):
        self.w = self.add_weight(shape=(input_shape[-1], 1),
                                 initializer='random_normal',
                                 trainable=True, dtype=np.float32)
        
        self.b = self.add_weight(shape=(1,),
                                 initializer='random_normal',
                                 trainable=True, dtype=np.float32)
        
    def call(self, inputs):
        return tf.matmul(inputs, self.w) + self.b

model = LinearRegressionModel6()

!rm -rf logs
model = LinearRegressionModel6()
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.02), 
           loss="mse", metrics=['mean_absolute_error'])

tb_callback = tf.keras.callbacks.TensorBoard('./logs', update_freq=1)


model.fit(X_train,y_train, epochs=100, batch_size=5, callbacks=[tb_callback], 
       verbose=0, validation_data=(X_val, y_val))

<keras.src.callbacks.History at 0x7fe918536a30>

You can also define your own optimizer (see this blog)

model.b.numpy(), model.w.numpy()[0]

(array([13.017648], dtype=float32), array([-0.7233677], dtype=float32))

predictions = model(X)
rmse = np.mean((predictions-y)**2)

plt.figure(figsize=(15,2));
plt.plot(model.history.history["loss"], label="train"); 
plt.plot(model.history.history["val_loss"], label="val"); 
plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse); plt.legend();
../_images/dc545bd502e7b65e5bbcca5d9262a6f61560035e5b57291313eb2dd10a4dbc29.png

Version 7: Using train_step \(\rightarrow\) control loss and gradients on a custom model.#

class LinearRegressionModel7(tf.keras.Model):
    
    def build(self, input_shape):
        self.w = self.add_weight(shape=(input_shape[-1], 1),
                                 initializer='random_normal',
                                 trainable=True, dtype=np.float32)
        
        self.b = self.add_weight(shape=(1,),
                                 initializer='random_normal',
                                 trainable=True, dtype=np.float32)
        
        self.loss_fn = tf.keras.metrics.MeanSquaredError()
        
    def call(self, inputs):
        return tf.matmul(inputs, self.w) + self.b

    def test_step(self, data):
        # here we implement loss by hand
        return {'loss': tf.reduce_mean((self(X)-y)**2)  }
    
    @tf.function
    def train_step(self, data):
        X,y = data
        loss_fn = lambda y_true, y_preds: tf.reduce_mean((y_true-y_preds)**2)
        with tf.GradientTape() as tape:
            # we use tf.keras loss function (equivalent to test_step)
            loss_fn = tf.keras.metrics.mean_squared_error
            loss = tf.reduce_mean(loss_fn(y, self(X)))
            
        grads = tape.gradient(loss, self.trainable_variables)
        self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
        
        return {'loss': loss}

model = LinearRegressionModel7()
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.02))
#model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.035))
model.fit(X_train,y_train, epochs=400, batch_size=5, verbose=0, validation_data=(X_val, y_val))

<keras.src.callbacks.History at 0x7fe969b2e6d0>

[i.numpy() for i in model.trainable_variables]

[array([[-0.67465234]], dtype=float32), array([12.980438], dtype=float32)]

predictions = model(X)
rmse = np.mean((predictions-y)**2)

plt.figure(figsize=(15,2));
plt.plot(model.history.history["loss"], label="train"); 
plt.plot(model.history.history["val_loss"], label="val"); 
plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse); plt.legend();
../_images/05f55dd036f4f6f93c58eda87c57e04d439d5ac73186ac4438e8db82a28dfd2b.png

Version 8: Using train_step \(\rightarrow\) control loss and gradients on a standard model.#

observe that:

  • we use a standard Dense layer,

  • we use a custom loss function and optimizer.apply_gradients

class CustomModel(tf.keras.Model):
    
    def test_step(self, data):
        return {'loss': tf.reduce_mean((self(X)-y)**2)}    
    
    @tf.function
    def train_step(self, data):
        X,y = data
        
        with tf.GradientTape() as tape:
            y_pred = self(X, training=True)
            loss_value = tf.reduce_mean((y_pred-y)**2)
            
        grads = tape.gradient(loss_value, self.trainable_variables)
        self.optimizer.apply_gradients(zip(grads, self.trainable_variables))
        
        return {'loss': loss_value}

from tensorflow.keras.layers import Dense, Input
    
def get_model8():
    
    inputs = tf.keras.layers.Input(shape=(1))
    outputs = tf.keras.layers.Dense(1, activation="linear")(inputs)
    
    model = CustomModel(inputs, outputs)
    
    model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.02))
    return model

our custom loop (for any model !!!)

model = get_model8()
model.summary()

Model: "custom_model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 1)]               0         
                                                                 
 dense_6 (Dense)             (None, 1)                 2         
                                                                 
=================================================================
Total params: 2 (8.00 Byte)
Trainable params: 2 (8.00 Byte)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

model.weights

[<tf.Variable 'dense_6/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[1.137009]], dtype=float32)>,
 <tf.Variable 'dense_6/bias:0' shape=(1,) dtype=float32, numpy=array([0.], dtype=float32)>]

model.trainable_variables

[<tf.Variable 'dense_6/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[1.137009]], dtype=float32)>,
 <tf.Variable 'dense_6/bias:0' shape=(1,) dtype=float32, numpy=array([0.], dtype=float32)>]

model.fit(X_train,y_train.reshape(-1,1), epochs=400, batch_size=5, verbose=0, validation_data=(X_val, y_val))

<keras.src.callbacks.History at 0x7fe95959cac0>

model.trainable_variables

[<tf.Variable 'dense_6/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[-0.9636562]], dtype=float32)>,
 <tf.Variable 'dense_6/bias:0' shape=(1,) dtype=float32, numpy=array([12.985804], dtype=float32)>]

predictions = model(X)
rmse = np.mean((predictions-y)**2)

plt.figure(figsize=(15,2));
plt.plot(model.history.history["loss"], label="train"); 
plt.plot(model.history.history["val_loss"], label="val"); 
plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse); plt.legend();
../_images/8a302e51524699c72fec37691e43c38a1f09553de197b6015c5b81ba68241ed9.png

Version 9: using train_on_batch \(\rightarrow\) control data#

epochs = 400
batch_size = 5

model = get_model8()
h = []
for epoch in tqdm(range(epochs)):
    idxs = np.random.permutation(len(X))
    for step in range(len(X)//batch_size+((len(X)%batch_size)!=0)):
        X_batch = X[idxs][step*batch_size:(step+1)*batch_size]
        y_batch = y[idxs][step*batch_size:(step+1)*batch_size]       
        model.train_on_batch(X_batch, y_batch)
    h.append(model.test_step([X_batch, y_batch])['loss'])

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 400/400 [00:48<00:00,  8.22it/s]

model.trainable_variables

[<tf.Variable 'dense_7/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[-0.15614377]], dtype=float32)>,
 <tf.Variable 'dense_7/bias:0' shape=(1,) dtype=float32, numpy=array([9.998391], dtype=float32)>]

predictions = model(X)

rmse = tf.reduce_mean((predictions-y)**2).numpy()
plt.figure(figsize=(15,2));
plt.plot(h); plt.xlabel("step number"); plt.ylabel("loss"); plt.grid();
plt.title("RMSE %.3f"%rmse);
../_images/b957bcdff4ad9078d4a9daf5e94145500fd94c4a6ca4ab083eb126edb7718639.png