Example_3_5#
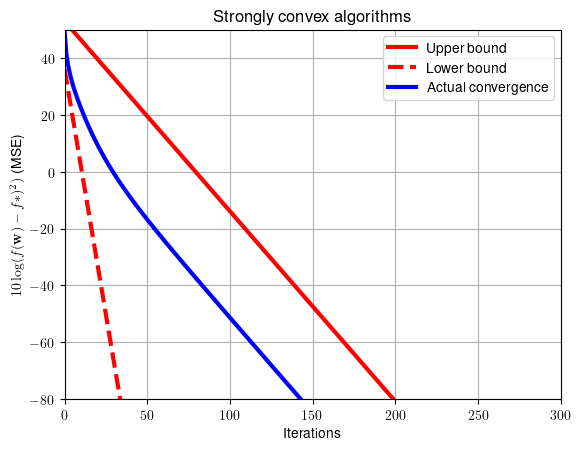
Testing convergence rate of strongly convex functions/algorithms
!wget --no-cache -O init.py -q https://raw.githubusercontent.com/jdariasl/OTBD/main/content/init.py
import init; init.init(force_download=False)
#!sudo apt install cm-super dvipng texlive-latex-extra texlive-latex-recommended
import numpy as np
from local.lib.utils import ridge_reg, bounds
import matplotlib.pyplot as plt
# Problem definition
Nc=500 # Number of columns
Nr=400 # Number of rows
Niter=400
X=np.random.randn(Nr,Nc)
wopt_nor=np.random.randn(Nc,1)
y=X@wopt_nor+np.random.randn(Nr,1)*np.sqrt(.001) # We generate the ragression data
autoval=np.real(np.linalg.eig(X.T@X)[0])
L=np.max(autoval)
lambd=0.04*L
wopt_strong=np.linalg.inv(X.T@X+lambd*np.eye(Nc))@X.T@y
Ls=np.max(autoval)+lambd
mu=np.min(np.abs(autoval))+lambd
eta=1/L
eta_strong=2/(Ls+mu)
# We calculate the bounds
_, _, _, bbs, bsm, _=bounds(Niter,L,Ls,mu,np.linalg.norm(wopt_nor)**2,np.linalg.norm(wopt_strong)**2)
# Ridge with regularizer
w=np.zeros((Nc,Niter+1))
f_r, f_opt = ridge_reg(Niter,w,X,y,eta_strong,lambd,wopt_strong)
plt.rcParams.update({
"text.usetex": True,
"font.family": "Helvetica"
})
plt.plot(range(Niter),10*np.log10(bbs),color='red',linewidth = 3, label = 'Upper bound')
plt.plot(range(Niter),10*np.log10(bsm),color='red',linestyle='dashed', linewidth = 3, label = 'Lower bound')
plt. plot(range(Niter+1),10*np.log10(np.abs(f_r-f_opt)+np.finfo(float).eps),'b', linewidth = 3, label = 'Actual convergence')
plt.legend()
plt.grid()
plt.title('Strongly convex algorithms')
plt.xlabel('Iterations')
plt.ylabel(r'$10\log(f({\bf{w}})-f*)^2)$ (MSE)')
plt.xlim([0, 300])
plt.ylim([-80, 50])
plt.show()